funciones matematicas

Colegio de bachilleres de chiapas

Plantel 06 reforma

Materia:

matematicas 4

Catedratico:

Miguel Angel Moscoso Lopez

Trabajo:

funciones matematicas

Integrantes:

Eliseo Soberano Cigarroa

Carlos Alberto Perez Ramos

Anthony Zea Luna

Sergio Jaret Notario Hernandez

grado:

4

grupo:

F

semestre:

2017-A

FUNCION ESCALONADA 

Denominamos como (Funciones escalonadas) a aquellas funciones que son definidas en un intervalo 
[a,b] finito de tal manera que sí mismas se encuentran definidas por medio de trozos (Segmentos), los cuales generan en un cierto sentido discontinuidades en la manera en la cual el comportamiento gráfico de una función se va dando.

Se representan como:  f(x)=[x] 

Como su nombre lo dice, su comportamiento gráfico genera la noción como si hubiera unos escalones proyectos es un plano (XY). Donde tales no necesariamente pueden tener un aspecto creciente, pueden tener un aspecto de decrecimiento también.

Dichas son creadas tomando la noción de cada cuando se presento una discontinuidad, lo cual da la posibilidad de definir la longitud de los segmentos a (Trozos).

Dentro de las nociones del analísis matemático existe un herramienta ejemplificada como una función base la cual nos da hincápie a la posibilidad de poder formular una función escalonada con facilidad, debido a que tal se basa en el criterio de una unidad de longitud en lo que respecta a los segmentos (trozos).

También una función escalonada es aquella función definida a trozos que en cualquier intervalo finito [a, b] en que esté definida tiene un número finito de discontinuidades c1 < c2 < ... < cn, y en cada intervalo ]ck, ck+1[ es constante, teniendo discontinuidades de salto en los puntos ck.

OTRA FORMA DE DECIRLO:

Informalmente, una función escalonada es aquella cuya gráfica tiene la forma de una escalera o una serie de escalones (que no necesariamente deben ser crecientes) al ser dibujada. El ejemplo más común de función escalonada es la función parte entera. Otras funciones escalonadas son la función unitaria de Heaviside o función escalón unitario, y la función signo.

La composición de cualquier función escalonada s(x) y una función cualquiera f(x) da por resultado una función escalonada g(x) = f(s(x)), siempre que f(x) esté definida para cualquier valor de x en el rango de s(x).

Evidentemente, la derivada de una función escalonada es 0 en cualquier punto en que se halle definida. No puede definirse en los puntos en que hay discontinuidades. lo que hace que una función sea escalonada son sus radicales de tipo a b c lo que hace que sea un poco más compleja.

En la tienda de la esquina de Macul con Grecia, hay una lista de precios para anillado: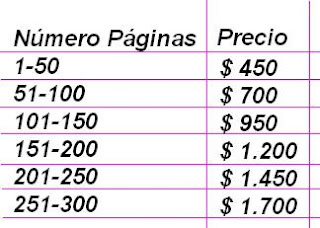Y si construimos la gráfica de esta función, resultará:

Esta función es conocida como Función Escalonada.

Veamos ahora otro ejemplo: Mire el siguiente letrero de estacionamiento:

Se ve de este ejemplo real, que muchas veces a números Reales se les debe asignar números enteros. Por ejemplo, tabto a 38 minutos como a 43,785 minutos se les asigna el valor de $ 900.
Desde aquí podemos nexar el concepto de una cierta función, llamada PARTE ENTERA, que asocia a cada valor Real el MAYOR DE LOS NÚMEROS ENTEROS QUE SON MENORES O IGUALES A EL.

La gráfica de esta Función es:

Ojo que en cada x natural, hay un especial cuidado. Fíjese que en x=1, la función está definida como f(1)=0, y hay un circulito señalizando vacío en y=1. Esto, ¿Por qué sucede? Porque estamos hablando de FUNCION parte entera, si para un valor de abcisa, hubiese 2 ordenadas, ya NO habría función 

                                           FUNCION: VALOR ABSOLUTO

El valor absoluto o módulo¹ de un numero real es su valor numerico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de +3 y de -3.

Una función de valor absoluto es una función que contiene una expresión algebraica dentro de los símbolos de valor absoluto. Recuerde que el valor absoluto de un número es su distancia desde 0 en la recta numérica .

La función padre de valor absoluto, escrita como f ( x ) = | x |, está definida como

                                              funcion: identidad

Una función identidad es una función tal que la imagen de cualquier elemento es éste mismo:

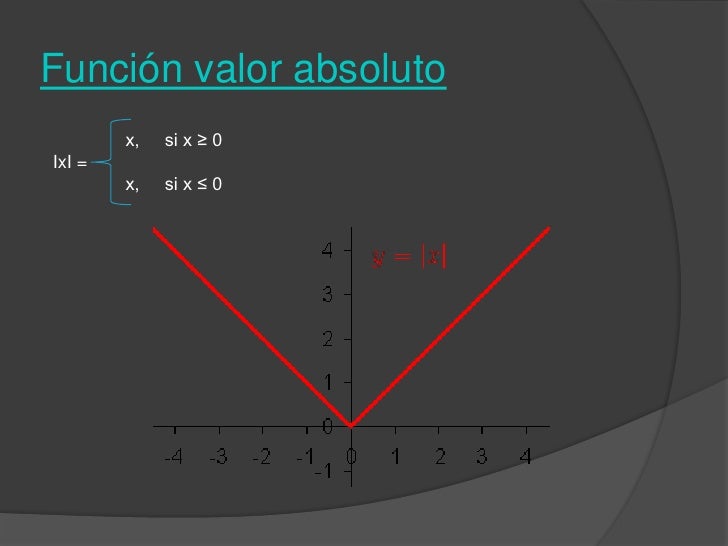
La función identidad también suele denotarse por id.

La función identidad es una función lineal de pendiente m = 1 que pasa por el origen de coordenadas, es decir, por el punto (0,0). Divide el primer y el tercer cuadrante en partes iguales, o sea, es su bisectriz.

La pendiente es la inclinación con respecto al eje X (eje de abscisas). Al ser ésta positiva (m > 0), la función es creciente.

Que la pendiente de la función identidad sea m = 1 significa que si aumentamos la x en una unidad, la y también aumenta en una unidad.

Formará un ángulo de 45° con cualquiera de los ejes.






funcion: constante

Una función f es constante si la variable dependiente y toma el mismo valor a para cualquier elemento del dominio (variable independiente x).

En términos matemáticos, la función f es constante si para cualquier par de puntos x₁ y x₂del dominio tales que x₁<x₂, se cumple que f(x₁) = f(x₂).

La gráfica de una función constante es una recta paralela al eje de abscisas X.

También se puede definir una función constante a partir de la derivada. Una función f será constante si para todo punto x del dominio la derivada es nula, es decir f ’(x) = 0.

La derivada de la función constante es 0 porque no depende del valor de la variable independiente x.